Tutorial: Bayesian Vector Autoregression Models
by Kevin Kotzé
1 The Bayesian VAR model with Minnesota prior
In this example we will model the long run behaviour of nonstationary time series with a Bayesian vector autoregressive model that makes use of a Minnesota prior. The model for this example is contained in the file T9_minn.R. To start off we can clear all the variables from the current environment and close all the plots.
rm(list = ls())
graphics.off()Thereafter, we will need to make use of the BMR package, which has a number of dependencies:
install.packages("Rcpp")
install.packages("ggplot2")
devtools::install_github("kthohr/BMR")To make use of the routines in the BMR package we need to make use of the library command.
library(BMR)As this data is contained in a .csv file we need to set the directory to tell R where to find the datafile. You will need to change the following extension to ensure that the correct path is specified.
setwd("C:\\Users\\image")This allows us to load the data and transform the price index to year-on-year inflation, we proceed as follows.
dat <- read.csv(file = "USdata.csv")To ensure that this has all been completed correctly, we can then plot the data, using the gtsplot command from within BMR.
gtsplot(dat[, 2:4], dates = dat[, 1])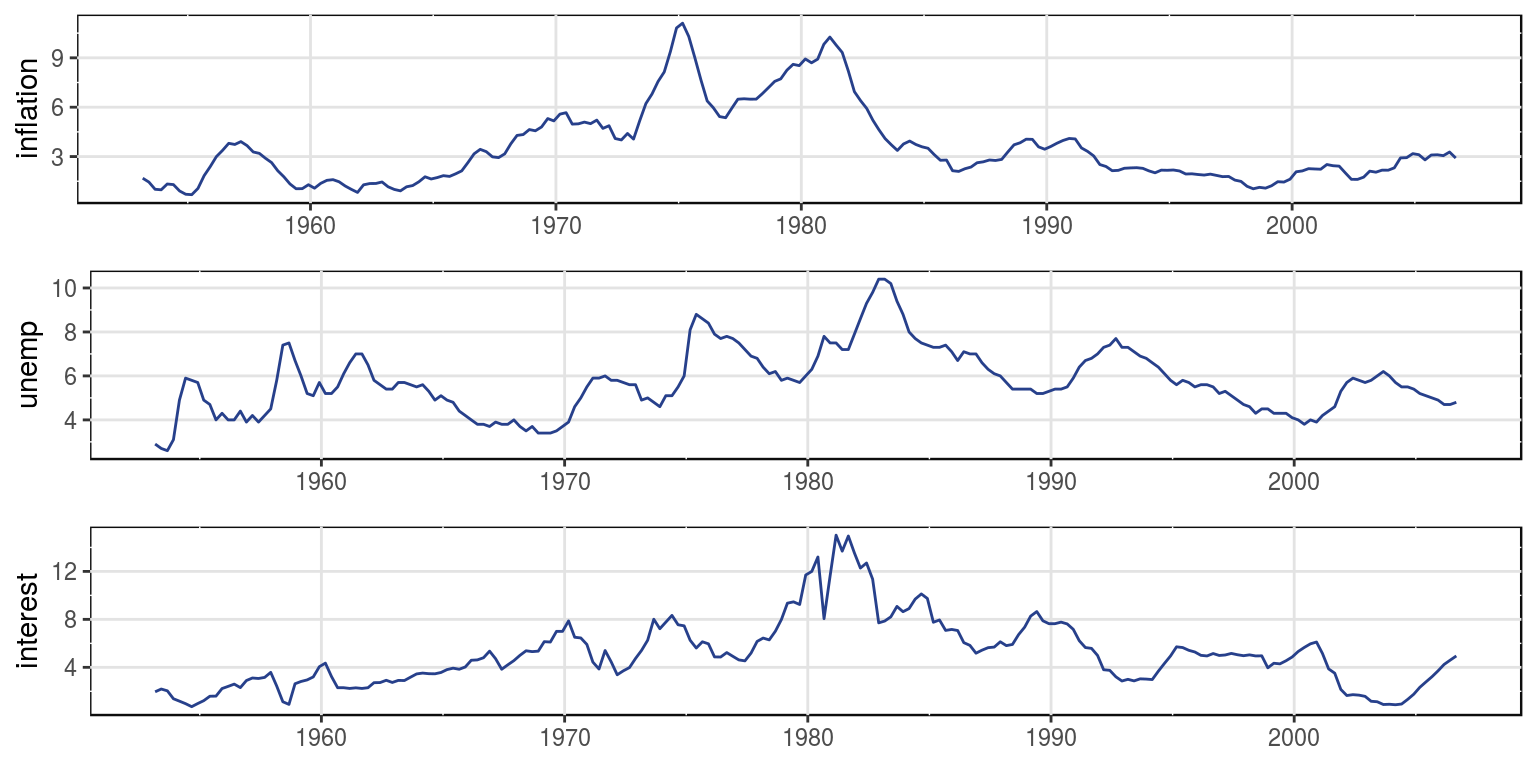
This graph would suggest that all the variables would potentially have a stochastic trend.
1.1 Model selection and estimation
We firstly need to create a model object that will store all the results from the estimation procedure. We can call this object bvar_obj.
bvar_obj <- new(bvarm)The basic structure of the model and the data need to be included in the build part of this object. In this case we are going to make use of a VAR(4) with a constant and the data that we will be using is stored in columns two through four.
bvar_obj$build(data.matrix(dat[,2:4]),
TRUE, # constant
4) # lagsTo use random-walk priors for the non-stationary variables, we set the prior mean values to unity before estimating the model parameters.
prior <- c(1, 1, 1)To complete the construction of the prior we need to select values for the hyperparameters. In this case we are going to follow @Canova:2007 and set the first hyperparameter, \(\lambda\), to 0.2 and the second hyperparameter, \(\theta\), to 0.5. He also recommends the values that were used for the second and third hyperparameters, HP2 and HP3. The other elements take on the default vaules that are taken from @Koop:2010.
bvar_obj$prior(prior, # prior mean value
1, # var_type
1, # decay_type
0.2, # HP1
0.5, # HP2
10^5, # HP3
1.0) # HP4The final requirement is to specify the number of draws that are required for the Gibbs sampler, which we are setting to 10,000 in this case.
bvar_obj$gibbs(10000)To plot the density functions for the parameter estimates we would then make use of the following commands.
plot(bvar_obj, var_names = colnames(dat)[-1], save = FALSE)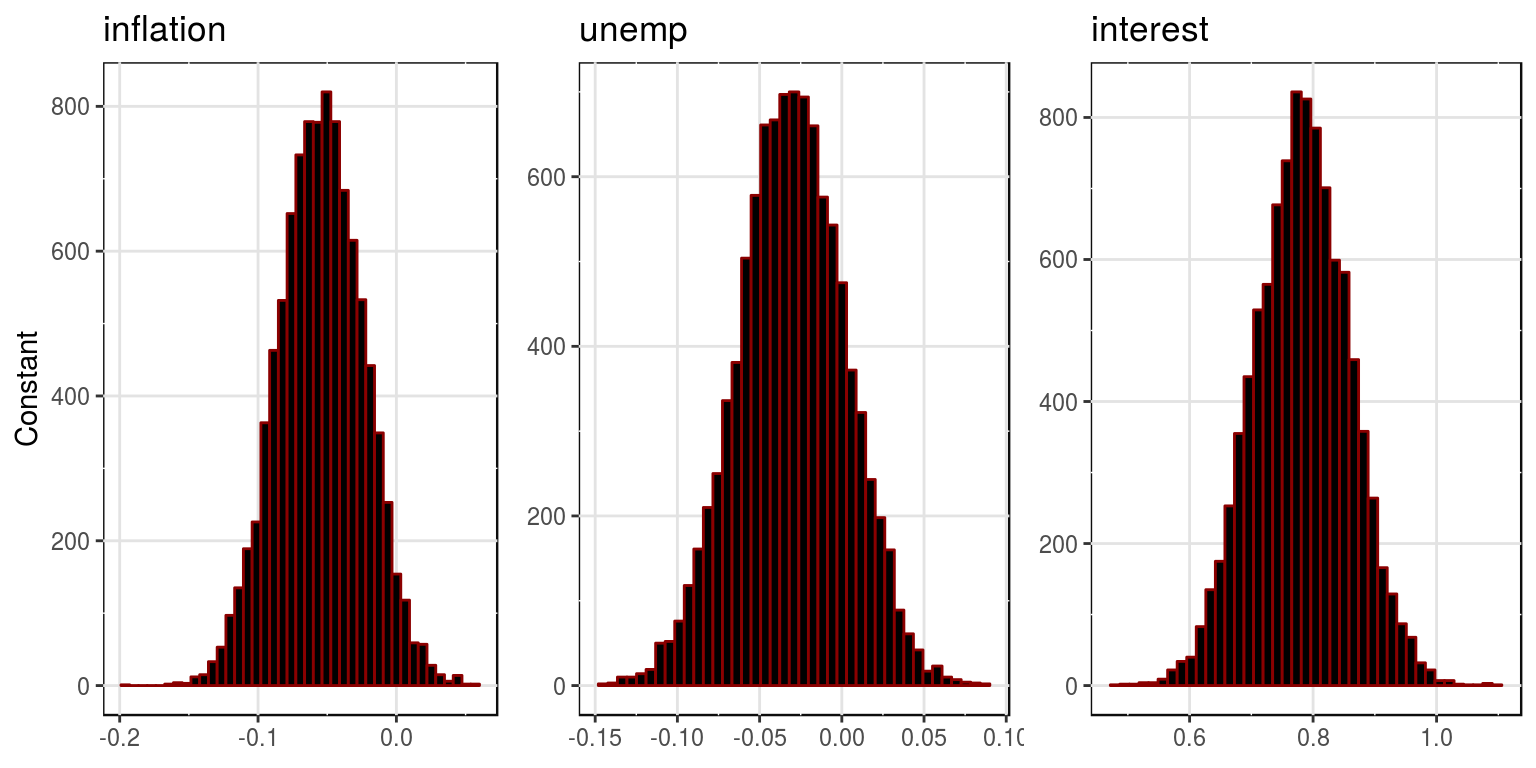
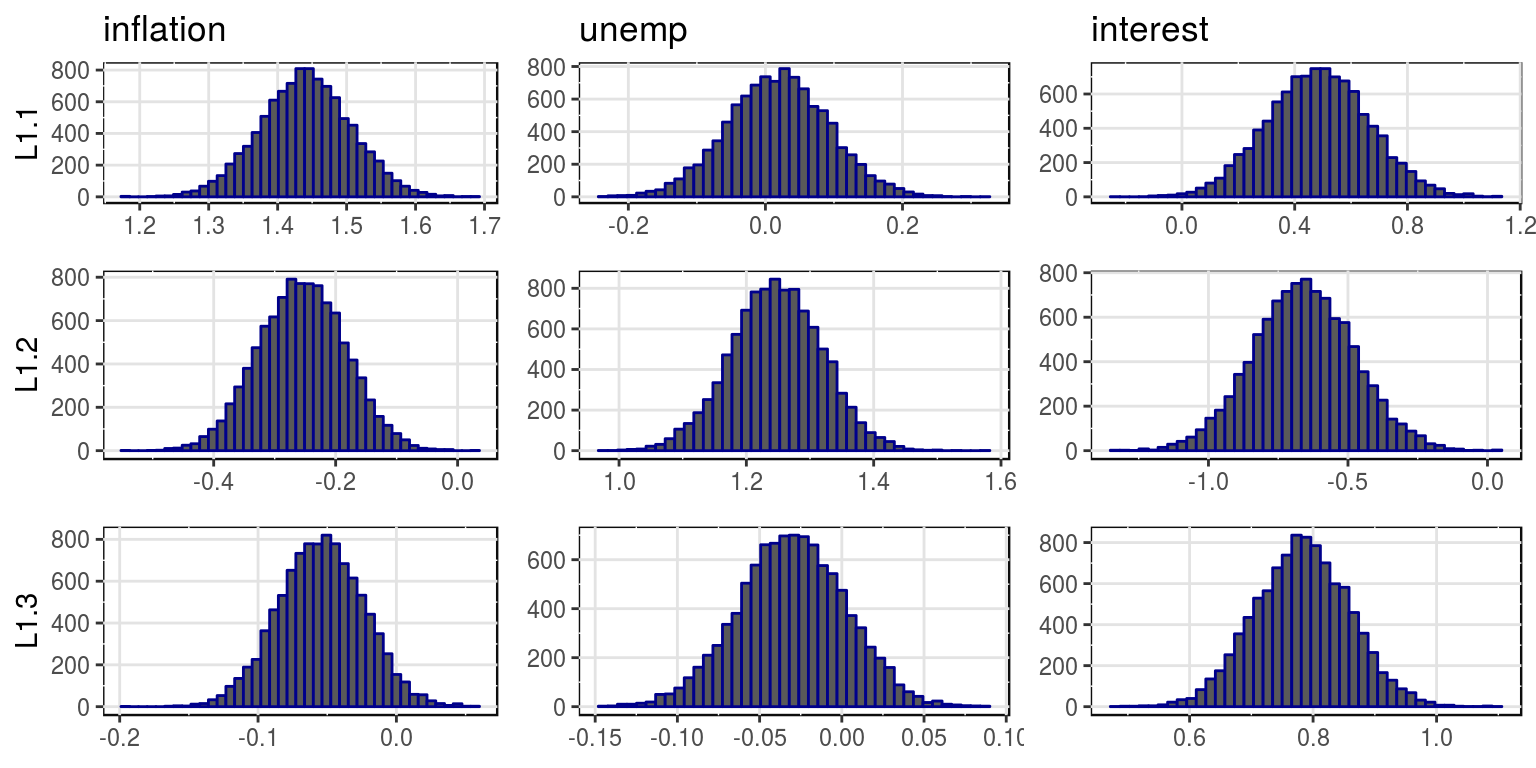
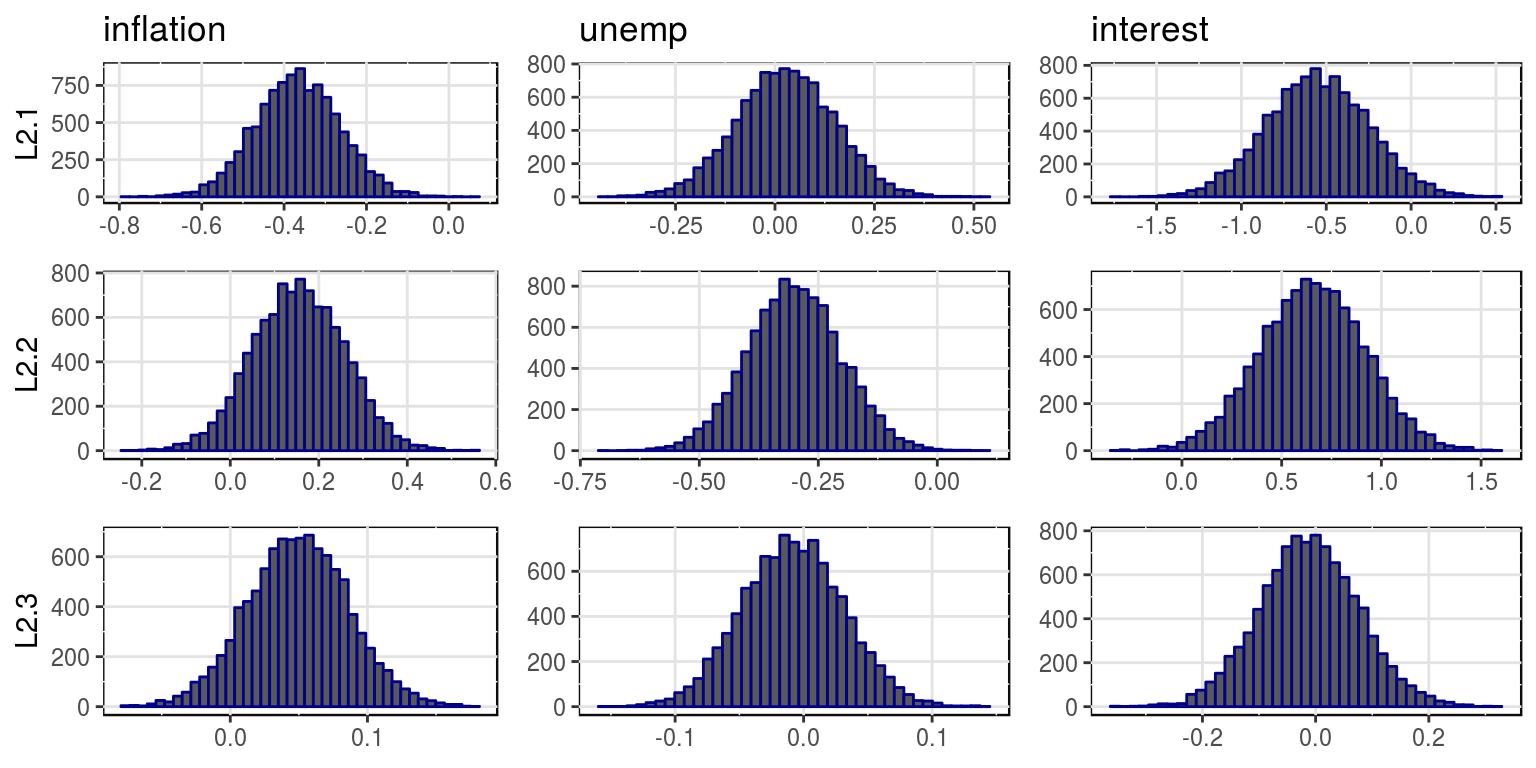
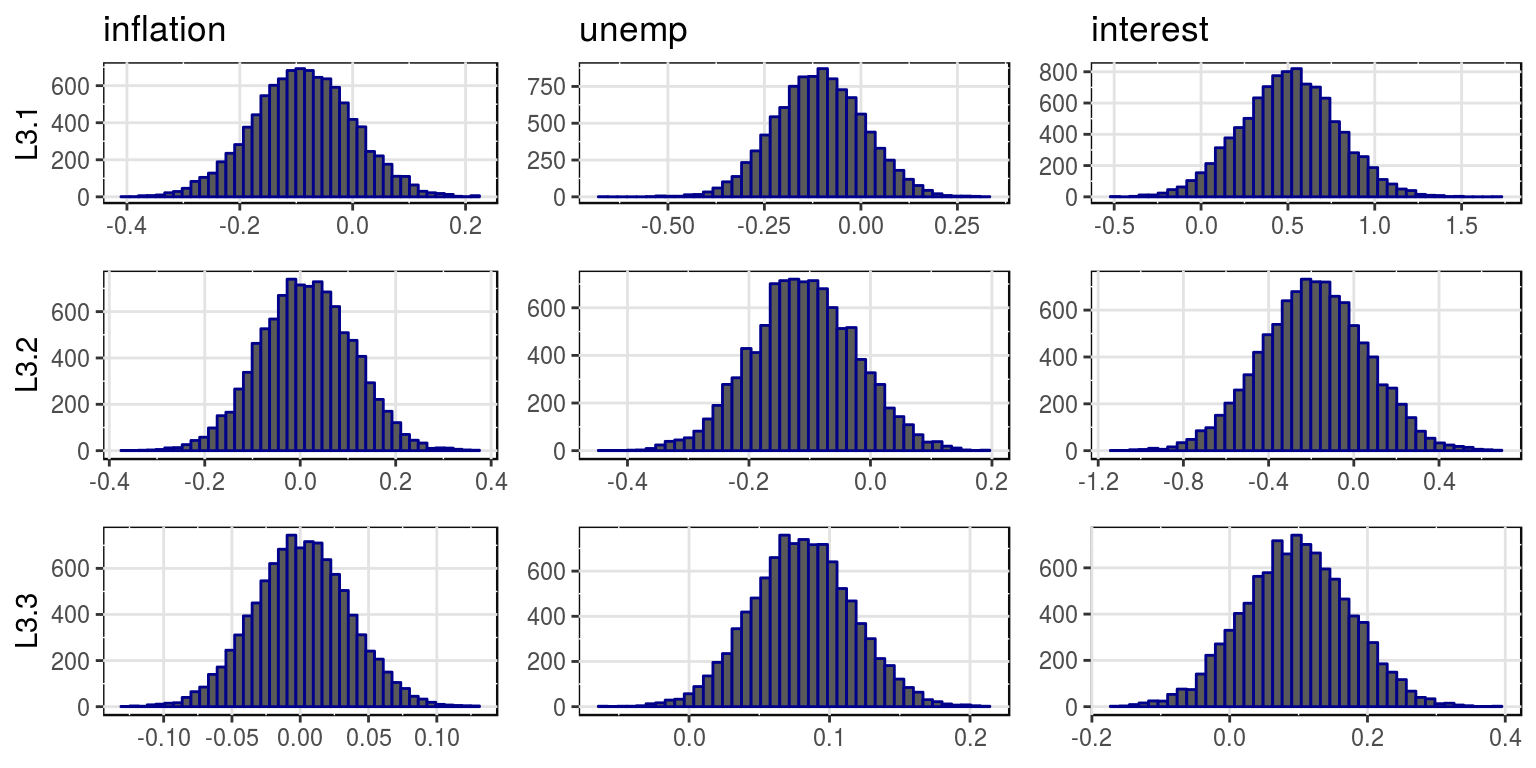
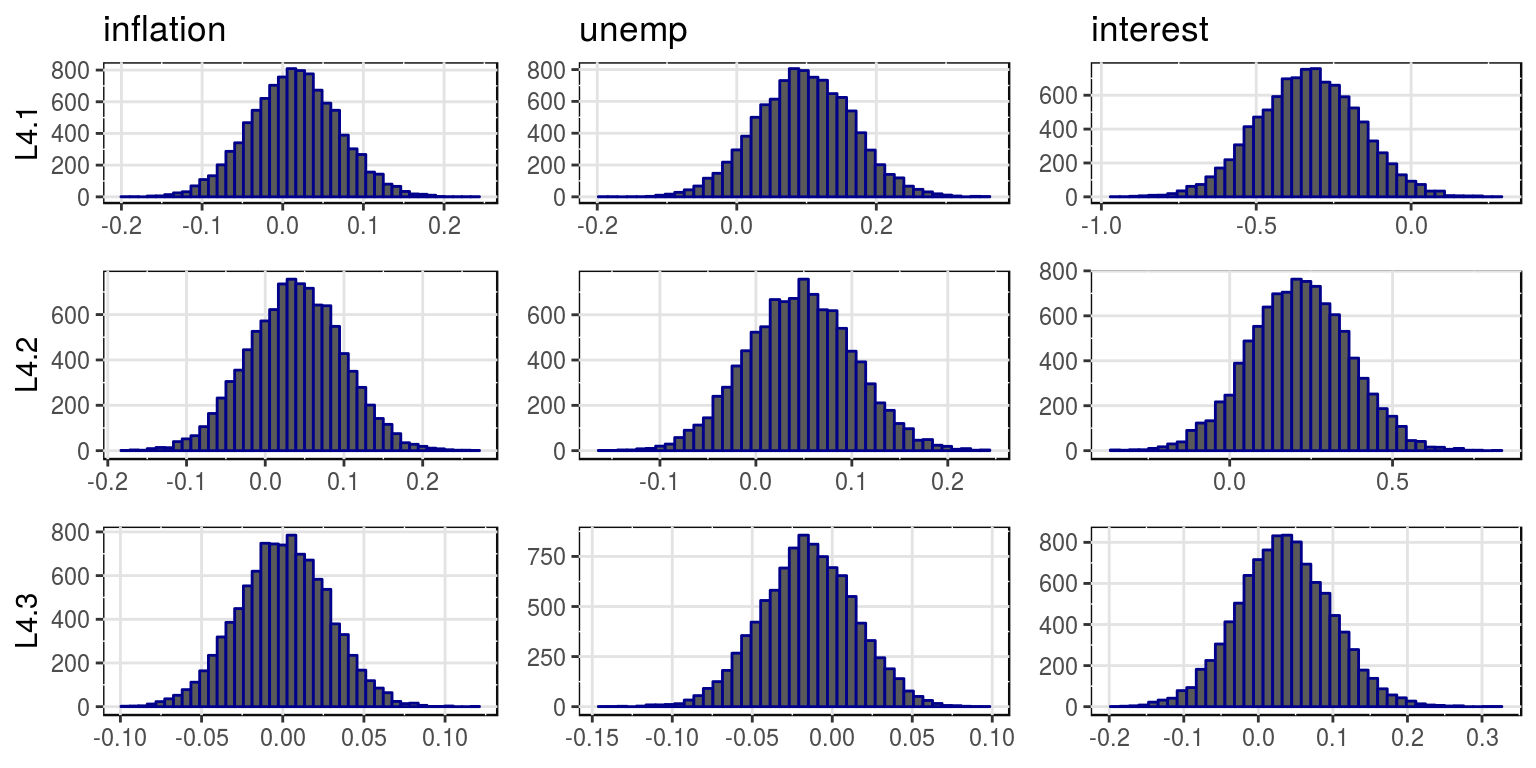
where the mean and variances for this distributions are stored in the objects, bvar_obj$alpha_pt_mean and bvar_obj$alpha_pt_var. And then the impulse response functions could be plotted as follows:
IRF(bvar_obj, 20, var_names = colnames(dat)[-1], save = FALSE)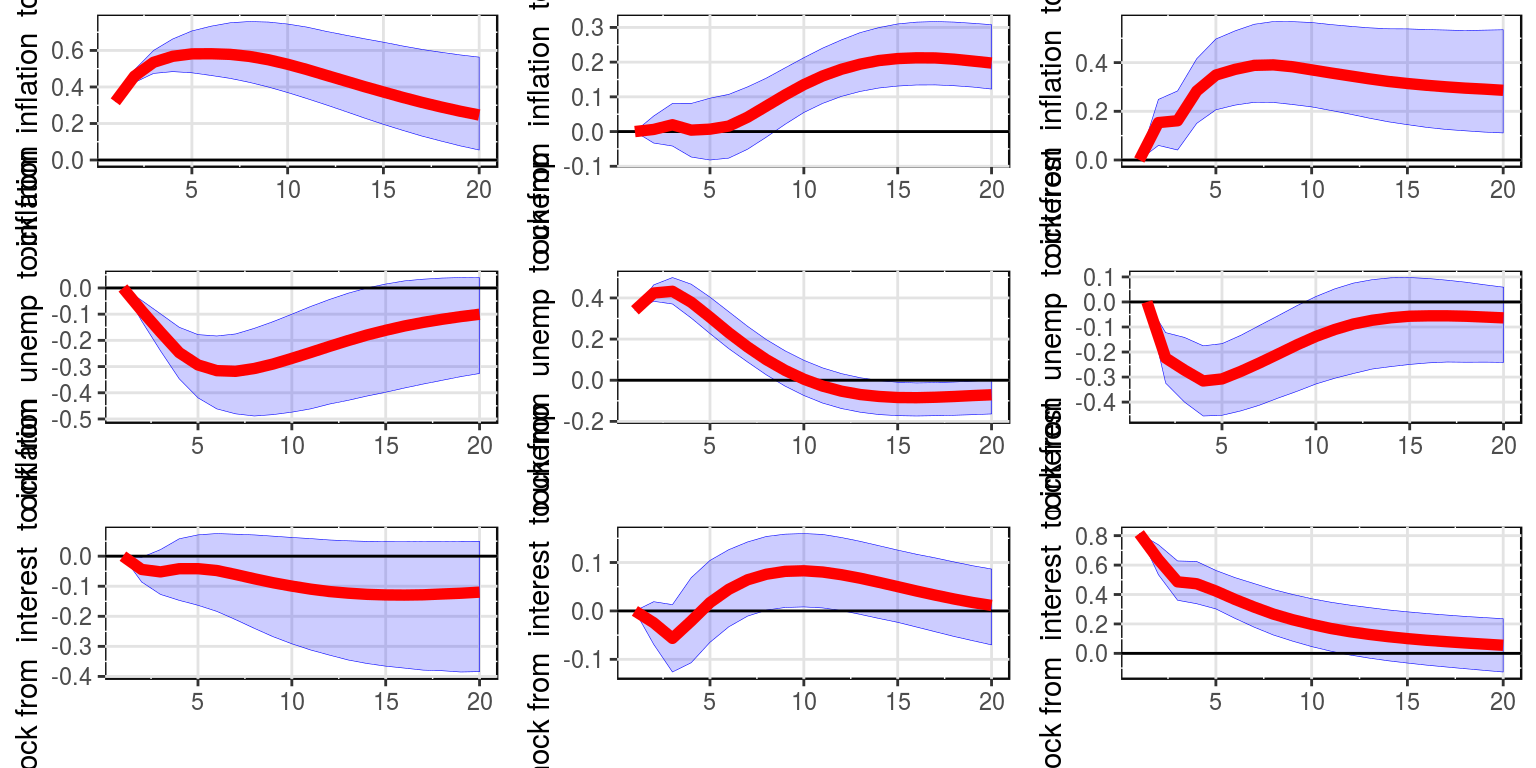
To generate forecasts for each of the variables then we proceed as follows, where shocks indicates that we would like to incorporate the effect of the shocks in estimation. The amount of back_data refers to the amount of observations to include in the graph prior to the initial forecasting point.
forecast(bvar_obj, shocks = TRUE, var_names = colnames(dat)[-1],
back_data = 12, save = FALSE)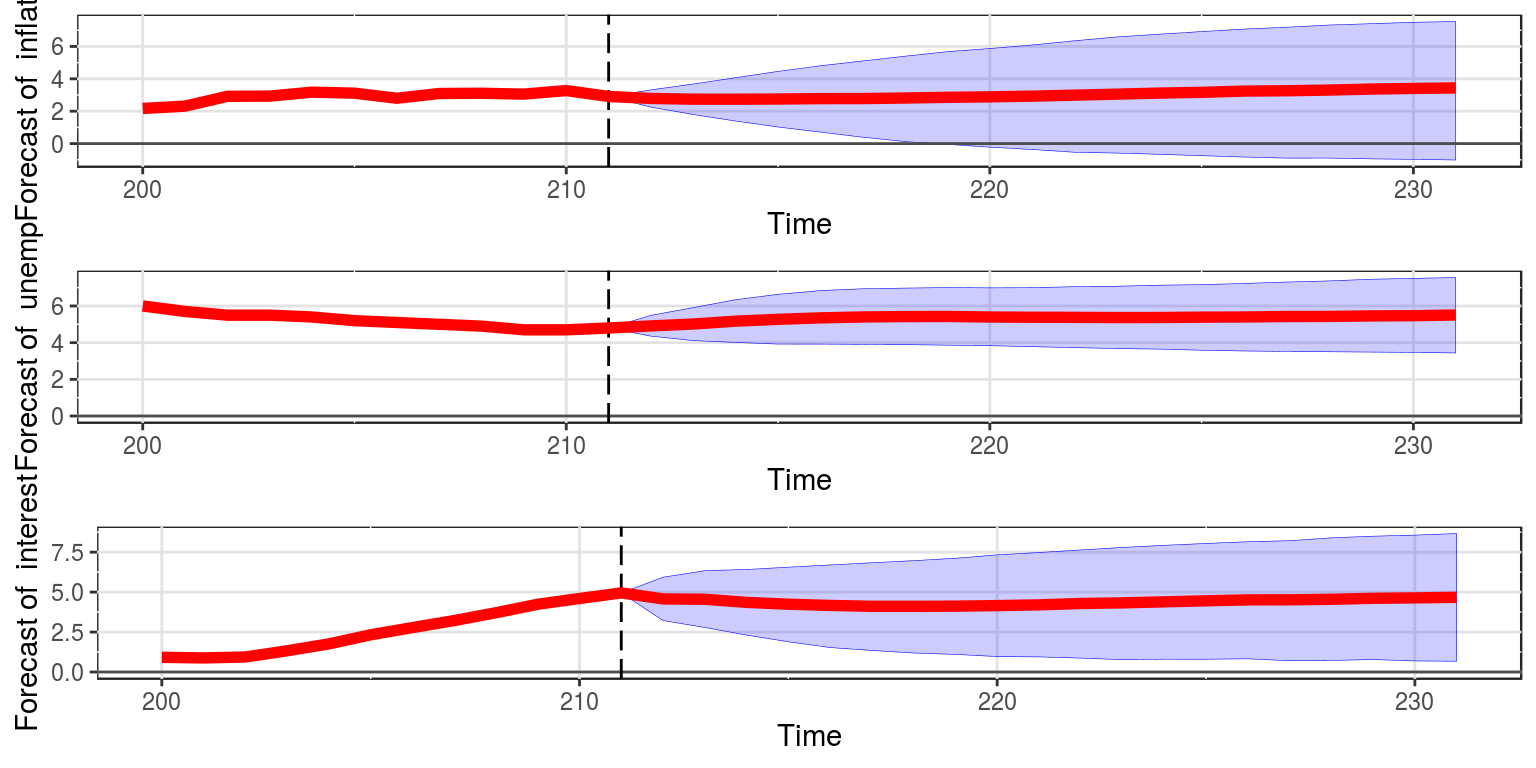
Note that the forecasts are future estimates of the trend in the process, and we are no longer forecasting time taken to return to trend. The specific values for the forecasts of the individual variables can be extracted from the object by amending the object to:
predict <- forecast(bvar_obj, shocks = TRUE, var_names = colnames(dat)[-1],
save = TRUE)2 Bayesian VARs with sign restrictions
The model for this example is contained in the file T9_sign.R. To start off we can clear all the variables from the current environment and close all the plots.
rm(list = ls())
graphics.off()Thereafter, we will need to make use of the VARsignR package that has been installed. If you need install this package, whcih is available on cran then you would want to run the following routine: install.packages("VARsignR").
library(VARsignR)As this data is contained in a .csv file we need to set the directory to tell R where to find the datafile. You will need to change the following extension to ensure that the correct path is specified.
setwd("C:\\Users\\image")This allows us to load the data and transform the price index to year-on-year inflation, we proceed as follows.
dat_raw <- read.csv(file = "uhlig_data.csv")
dat <- as.ts(dat_raw[, 2:7], start = c(1959, 1), frequency = 12)To ensure that this has all been completed correctly, we can then plot the data, using the gtsplot command from within BMR.
plot(dat)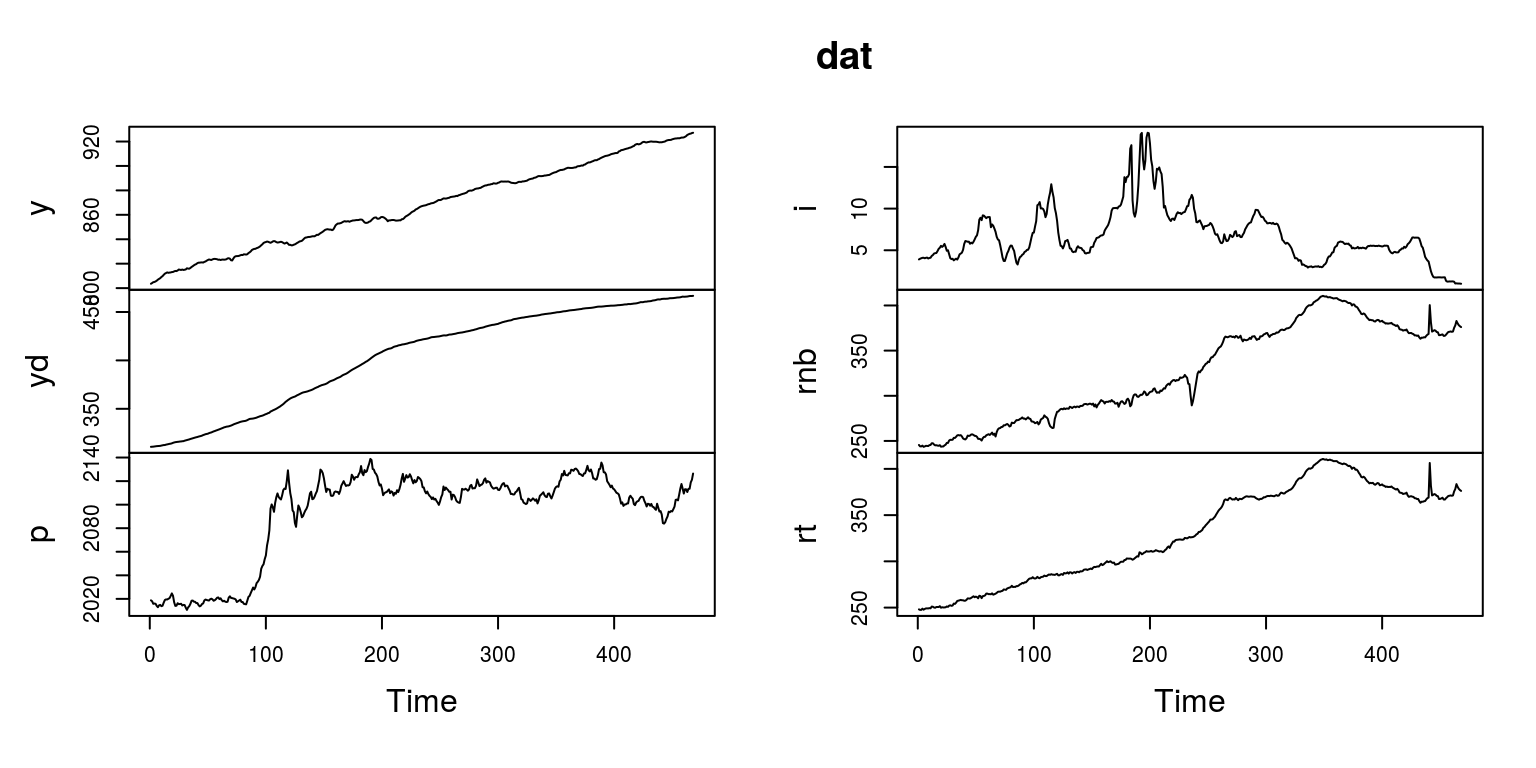
3 Uhlig (2005) rejection method
In terms of the restrictions we want to impose the following:
- Fourth variable: do not decrease the FED’s policy rate for \(x\) months after the shock
- Third variable: do not increase commodity prices for \(x\) months after the shock
- Second variable: do not increase inflation for \(x\) months after the shock
- Fifth variable: do not increase non-borrowed reserves for \(x\) months after the shock
Hence the constraint would take the form:
constr <- c(+4, -3, -2, -5)To replicate the results of @Uhlig:2005 we would then make use of a VAR(12) and no constant in the model. To generate the impulse response functions we make use of 60 steps. We use 200 draws from the posterior and 200 sub-draws for each posterior draw to generate the impulse vectors and the candidate impulse responses to which the rejection algorithm will be applied.
model1 <- uhlig.reject(Y = dat, nlags = 12, draws = 200,
subdraws = 200, nkeep = 1000, KMIN = 1, KMAX = 6, constrained = constr,
constant = FALSE, steps = 60)##
|
| | 0%
|
| | 1%
|
|= | 2%
|
|= | 3%
|
|== | 4%
|
|== | 5%
|
|== | 6%
|
|=== | 6%
|
|=== | 7%
|
|=== | 8%
|
|==== | 8%
|
|==== | 9%
|
|==== | 10%
|
|===== | 10%
|
|===== | 11%
|
|===== | 12%
|
|====== | 12%
|
|====== | 13%
|
|====== | 14%
|
|======= | 14%
|
|======= | 15%
|
|======= | 16%
|
|======== | 17%
|
|======== | 18%
|
|========= | 19%
|
|========= | 20%
|
|========= | 21%
|
|========== | 22%
|
|========== | 23%
|
|=========== | 24%
|
|=========== | 25%
|
|=========== | 26%
|
|============ | 26%
|
|============ | 27%
|
|============ | 28%
|
|============= | 28%
|
|============= | 29%
|
|============= | 30%
|
|============== | 30%
|
|============== | 31%
|
|============== | 32%
|
|=============== | 32%
|
|=============== | 33%
|
|=============== | 34%
|
|================ | 34%
|
|================ | 35%
|
|================ | 36%
|
|================= | 37%
|
|================= | 38%
|
|================== | 39%
|
|================== | 40%
|
|================== | 41%
|
|=================== | 42%
|
|=================== | 43%
|
|==================== | 44%
|
|==================== | 45%
|
|==================== | 46%summary(model1)## Length Class Mode
## IRFS 360000 -none- numeric
## FEVDS 360000 -none- numeric
## SHOCKS 456000 -none- numeric
## BDraws 38880 -none- numeric
## SDraws 3240 -none- numericThe results of the model are then provided as a result of the summary command, which gives an indication of what has been stored in the object model1. To plot the impulse response functions we would first give the variables names before creating an object irfs1. Thereafter, we would make use of the irfplot command to display the result:
nam <- c("GDP", "GDP Deflator", "Comm Price Index", "Fed Funds Rate",
"NB Reserves", "Total Reserves")
irfs1 <- model1$IRFS
irfplot(irfdraws = irfs1, type = "median", labels = nam,
save = FALSE, bands = c(0.16, 0.84), grid = TRUE, bw = FALSE)Note that in this case we have used confidence intervals of 16%. We could also plot the forecast-error variance decomposition using a similar procedure, where the object fevd1 contains the results and fevdplot displays these results in a graph.
fevd1 <- model1$FEVDS
fevdplot(fevd1, label = nam, save = FALSE, bands = c(0.16,
0.84), grid = TRUE, bw = FALSE, table = FALSE, periods = NULL)As an alternative we could display the results in a table, by making use of the following commands:
fevd.table <- fevdplot(fevd1, table = TRUE, label = nam,
periods = c(1, 10, 20, 30, 40, 50, 60))
print(fevd.table)## GDP GDP Deflator Comm Price Index Fed Funds Rate
## 1 8.86 6.91 7.18 10.17
## 10 9.52 8.16 8.00 12.53
## 20 12.06 9.22 8.33 12.96
## 30 13.11 9.46 8.72 12.93
## 40 12.67 9.62 9.22 12.84
## 50 12.40 9.79 9.56 12.72
## 60 12.19 9.94 9.93 12.66
## NB Reserves Total Reserves
## 1 5.72 7.73
## 10 8.82 8.57
## 20 10.23 9.57
## 30 10.26 9.75
## 40 10.34 9.95
## 50 10.49 10.02
## 60 10.57 10.17To recover the shocks we would need to extract the relevant information that is stored in the model object. Note that we have kept 1000 simulations, so we use the quantile function to generate confidence intervals for these shocks. These may be stored as a time series object, where we lost the first 12 observations as a part of the estimation procedure.
shocks <- model1$SHOCKS
ss <- ts(t(apply(shocks, 2, quantile, probs = c(0.5, 0.16,
0.84))), frequency = 12, start = c(1960, 1))To plot the result, we could make use of the following commands:
plot(ss[, 1], type = "l", col = "blue", ylab = "Interest rate shock",
ylim = c(min(ss), max(ss)))
abline(h = 0, col = "black")
lines(ss[, 2], col = "red")
lines(ss[, 3], col = "red")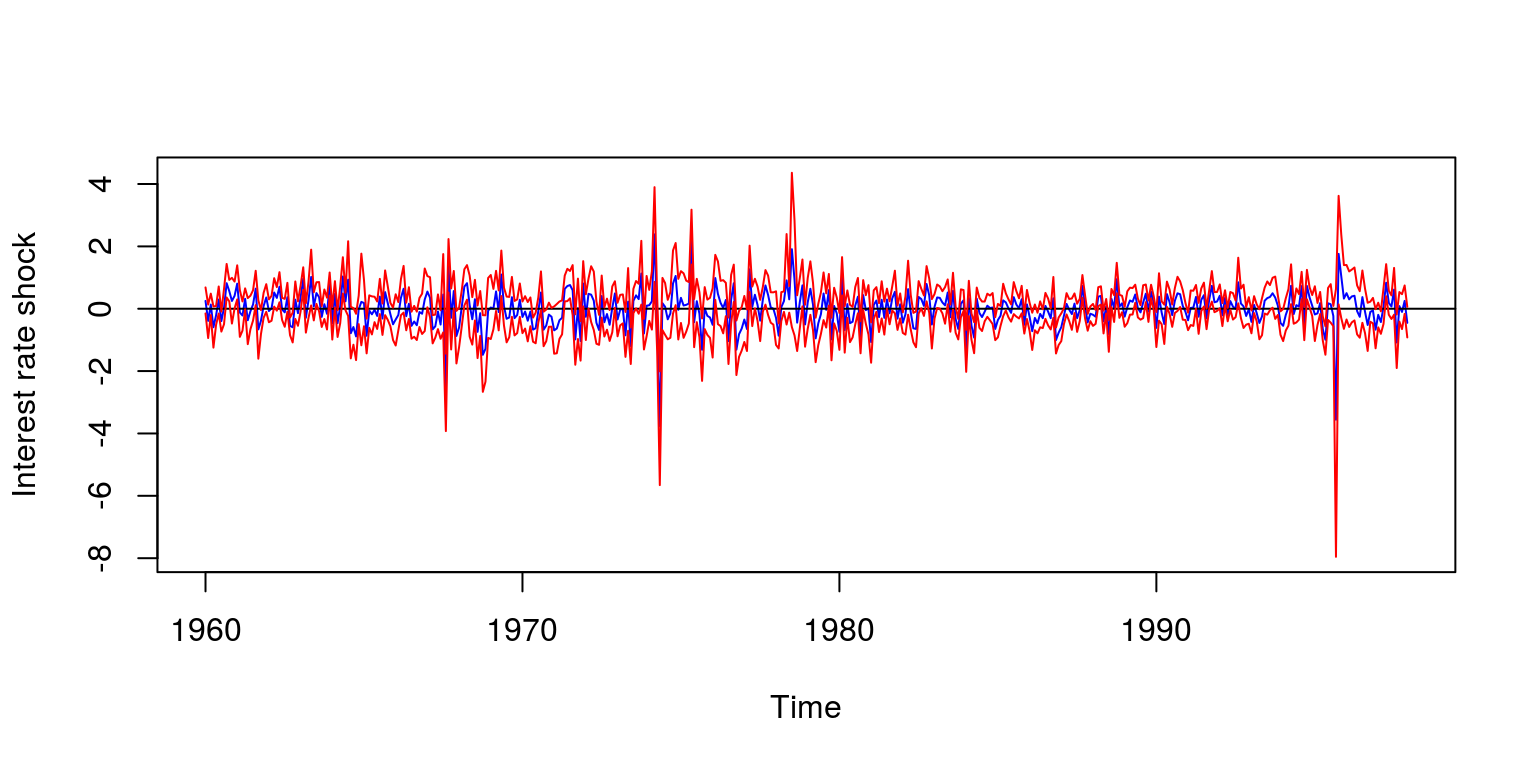
3.1 Rubio rejection
model2 <- rwz.reject(Y = dat, nlags = 12, draws = 200, subdraws = 200,
nkeep = 1000, KMIN = 1, KMAX = 6, constrained = constr,
constant = FALSE, steps = 60)##
|
| | 0%
|
| | 1%
|
|= | 2%
|
|= | 3%
|
|== | 4%
|
|== | 5%
|
|== | 6%
|
|=== | 6%
|
|=== | 7%
|
|=== | 8%
|
|==== | 8%
|
|==== | 9%
|
|==== | 10%
|
|===== | 10%
|
|===== | 11%
|
|===== | 12%
|
|====== | 12%
|
|====== | 13%
|
|====== | 14%
|
|======= | 14%
|
|======= | 15%
|
|======= | 16%
|
|======== | 17%
|
|======== | 18%
|
|========= | 19%
|
|========= | 20%
|
|========= | 21%
|
|========== | 22%
|
|========== | 23%
|
|=========== | 24%
|
|=========== | 25%
|
|=========== | 26%
|
|============ | 26%
|
|============ | 27%
|
|============ | 28%
|
|============= | 28%
|
|============= | 29%
|
|============= | 30%
|
|============== | 30%
|
|============== | 31%
|
|============== | 32%
|
|=============== | 32%
|
|=============== | 33%
|
|=============== | 34%
|
|================ | 34%
|
|================ | 35%
|
|================ | 36%
|
|================= | 37%
|
|================= | 38%
|
|================== | 39%
|
|================== | 40%
|
|================== | 41%
|
|=================== | 42%
|
|=================== | 43%
|
|==================== | 44%
|
|==================== | 45%
|
|==================== | 46%
|
|===================== | 46%
|
|===================== | 47%
|
|===================== | 48%
|
|====================== | 48%
|
|====================== | 49%
|
|====================== | 50%
|
|======================= | 50%
|
|======================= | 51%
|
|======================= | 52%
|
|======================== | 52%
|
|======================== | 53%
|
|======================== | 54%
|
|========================= | 54%
|
|========================= | 55%
|
|========================= | 56%
|
|========================== | 57%
|
|========================== | 58%
|
|=========================== | 59%
|
|=========================== | 60%
|
|=========================== | 61%
|
|============================ | 62%
|
|============================ | 63%
|
|============================= | 64%
|
|============================= | 65%
|
|============================= | 66%
|
|============================== | 66%
|
|============================== | 67%
|
|============================== | 68%
|
|=============================== | 68%
|
|=============================== | 69%
|
|=============================== | 70%
|
|================================ | 70%
|
|================================ | 71%
|
|================================ | 72%
|
|================================= | 72%
|
|================================= | 73%
|
|================================= | 74%
|
|================================== | 74%
|
|================================== | 75%
|
|================================== | 76%
|
|=================================== | 77%
|
|=================================== | 78%
|
|==================================== | 79%
|
|==================================== | 80%
|
|==================================== | 81%
|
|===================================== | 82%
|
|===================================== | 83%
|
|====================================== | 84%
|
|====================================== | 85%
|
|====================================== | 86%
|
|======================================= | 86%
|
|======================================= | 87%irfs2 <- model2$IRFS
irfplot(irfdraws = irfs2, type = "median", labels = nam,
save = FALSE, bands = c(0.16, 0.84), grid = TRUE, bw = FALSE)3.2 Uhlig penalty
model3 <- uhlig.penalty(Y = dat, nlags = 12, draws = 2000,
subdraws = 1000, nkeep = 1000, KMIN = 1, KMAX = 6, constrained = constr,
constant = FALSE, steps = 60, penalty = 100, crit = 0.001)##
|
| | 0%
|
| | 1%
|
|= | 1%
|
|= | 2%
|
|= | 3%
|
|== | 3%
|
|== | 4%
|
|== | 5%
|
|== | 6%
|
|=== | 6%
|
|=== | 7%
|
|=== | 8%
|
|==== | 8%
|
|==== | 9%
|
|==== | 10%
|
|===== | 10%
|
|===== | 11%
|
|===== | 12%
|
|====== | 12%
|
|====== | 13%
|
|====== | 14%
|
|======= | 14%
|
|======= | 15%
|
|======= | 16%
|
|======= | 17%
|
|======== | 17%
|
|======== | 18%
|
|======== | 19%
|
|========= | 19%
|
|========= | 20%
|
|========= | 21%
|
|========== | 21%
|
|========== | 22%
|
|========== | 23%
|
|=========== | 23%
|
|=========== | 24%
|
|=========== | 25%
|
|=========== | 26%
|
|============ | 26%
|
|============ | 27%
|
|============ | 28%
|
|============= | 28%
|
|============= | 29%
|
|============= | 30%
|
|============== | 30%
|
|============== | 31%
|
|============== | 32%
|
|=============== | 32%
|
|=============== | 33%
|
|=============== | 34%
|
|================ | 34%
|
|================ | 35%
|
|================ | 36%
|
|================ | 37%
|
|================= | 37%
|
|================= | 38%
|
|================= | 39%
|
|================== | 39%
|
|================== | 40%
|
|================== | 41%
|
|=================== | 41%
|
|=================== | 42%
|
|=================== | 43%
|
|==================== | 43%
|
|==================== | 44%
|
|==================== | 45%
|
|==================== | 46%
|
|===================== | 46%
|
|===================== | 47%
|
|===================== | 48%
|
|====================== | 48%
|
|====================== | 49%
|
|====================== | 50%irfs3 <- model3$IRFS
irfplot(irfdraws = irfs3, type = "median", labels = nam,
save = FALSE, bands = c(0.16, 0.84), grid = TRUE, bw = FALSE)3.3 Alternative restrictions
constr5 <- c(+4, -3, -2, -5, -6)model5c <- uhlig.reject(Y = dat, nlags = 12, draws = 200,
subdraws = 200, nkeep = 1000, KMIN = 1, KMAX = 6, constrained = constr5,
constant = FALSE, steps = 60)##
|
| | 0%
|
| | 1%
|
|= | 2%
|
|= | 3%
|
|== | 4%
|
|== | 5%
|
|== | 6%
|
|=== | 6%
|
|=== | 7%
|
|=== | 8%
|
|==== | 8%
|
|==== | 9%
|
|==== | 10%
|
|===== | 10%
|
|===== | 11%
|
|===== | 12%
|
|====== | 12%
|
|====== | 13%
|
|====== | 14%
|
|======= | 14%
|
|======= | 15%
|
|======= | 16%
|
|======== | 17%
|
|======== | 18%
|
|========= | 19%
|
|========= | 20%
|
|========= | 21%
|
|========== | 22%
|
|========== | 23%
|
|=========== | 24%
|
|=========== | 25%
|
|=========== | 26%
|
|============ | 26%
|
|============ | 27%
|
|============ | 28%
|
|============= | 28%
|
|============= | 29%
|
|============= | 30%
|
|============== | 30%
|
|============== | 31%
|
|============== | 32%
|
|=============== | 32%
|
|=============== | 33%
|
|=============== | 34%
|
|================ | 34%
|
|================ | 35%
|
|================ | 36%
|
|================= | 37%
|
|================= | 38%
|
|================== | 39%
|
|================== | 40%
|
|================== | 41%
|
|=================== | 42%
|
|=================== | 43%
|
|==================== | 44%
|
|==================== | 45%
|
|==================== | 46%
|
|===================== | 46%
|
|===================== | 47%
|
|===================== | 48%
|
|====================== | 48%
|
|====================== | 49%
|
|====================== | 50%
|
|======================= | 50%
|
|======================= | 51%
|
|======================= | 52%
|
|======================== | 52%
|
|======================== | 53%
|
|======================== | 54%
|
|========================= | 54%
|
|========================= | 55%
|
|========================= | 56%
|
|========================== | 57%
|
|========================== | 58%
|
|=========================== | 59%
|
|=========================== | 60%
|
|=========================== | 61%
|
|============================ | 62%
|
|============================ | 63%
|
|============================= | 64%irf5c <- model5c$IRFS
irfplot(irf5c, labels = nam)3.4 Comparison
fp.target(Y = dat, irfdraws = irfs1, nlags = 12, constant = F,
labels = nam, target = TRUE, type = "median", bands = c(0.16,
0.84), save = FALSE, grid = TRUE, bw = FALSE, legend = TRUE,
maxit = 1000)